
Calcul scientifique TP4 : Eléments finis
B. Aoubiza & M.R. Laydi ENS2M

On considère le problème à données régulières
suivant
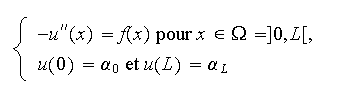
dont la formulation variationnelle est
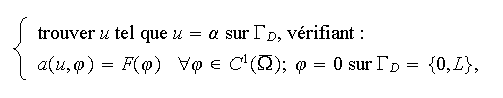
où


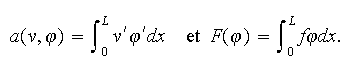
On note

![]() ,
l'espace des polynômes de degré
,
l'espace des polynômes de degré

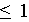 ,
i.e.
,
i.e.

![]() est l'espace engendré par les monômes
est l'espace engendré par les monômes

![]()
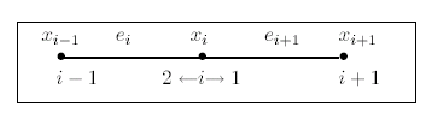
On découpe

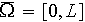 en
en

![]() intervalles
intervalles

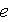 de longueur
de longueur

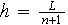 et on pose
et on pose

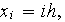

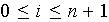 .
.

Sur chaque élément

![]() ,
tout polynôme de degré
,
tout polynôme de degré

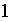

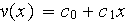 ,
,

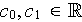 ,
s'écrit
,
s'écrit

Posons

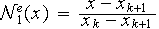 et
et

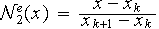 dont les graphes sont :
dont les graphes sont :
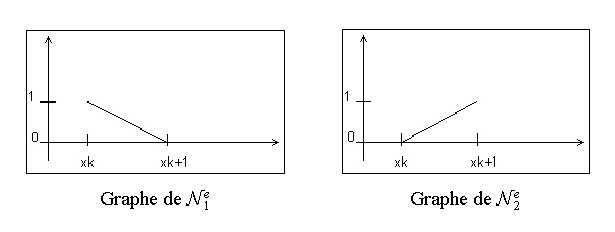
on
obtient
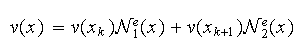
Introduisons les fonctions de base

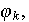

 ,
définies par
,
définies par
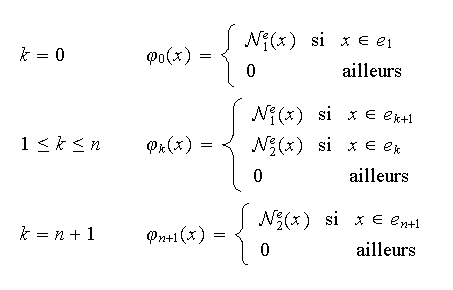
Remarquer que

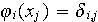 pour
pour 
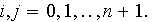
On note

![]() l'espace engendré par les fonctions de base
l'espace engendré par les fonctions de base



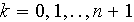 .
Donc
.
Donc

![]() et
et
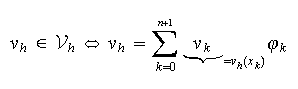
Le problème approché consiste à chercher
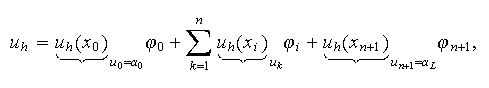
vérifiant

i.e.
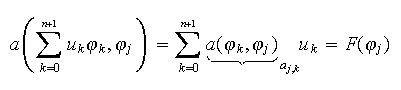
Le
problème est donc de trouver

![]() tel que
tel que
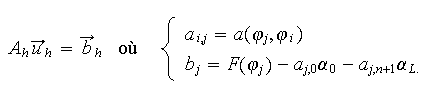
Calculons les coefficients du système ci-dessus qui sont donnés par
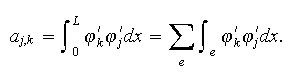
Comme

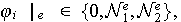 on obtient pour
on obtient pour

![]()
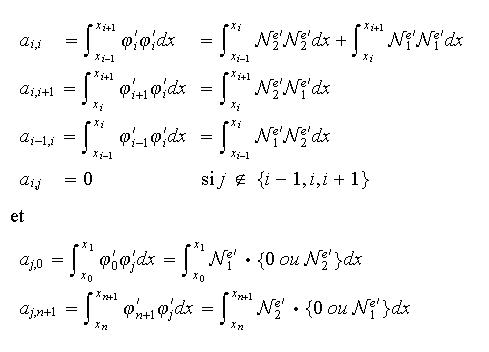
Ainsi le calcul des

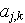 revient à évaluer pour chaque élément
revient à évaluer pour chaque élément

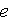 la matrice élémentaire
la matrice élémentaire
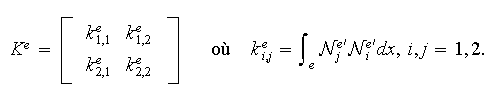
et
donc
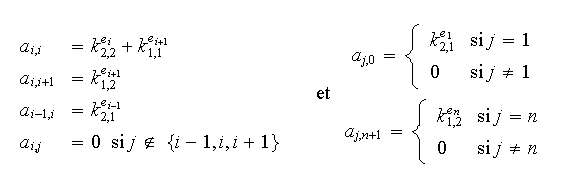
Calculons maintenant les composantes du second membre du système
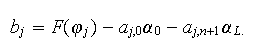
Le
terme

![]() est défini par
est défini par

Comme

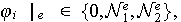 le calcul des
le calcul des

![]() revient à évaluer le second membre élémentaire
revient à évaluer le second membre élémentaire
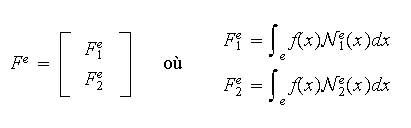
Ainsi,
on obtient

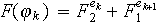
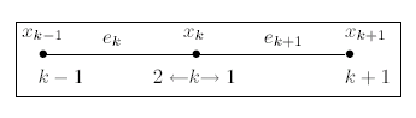
Donc
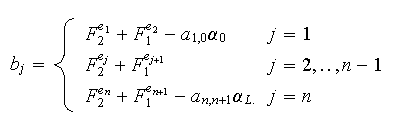
Pour le maillage ci-dessous où

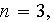
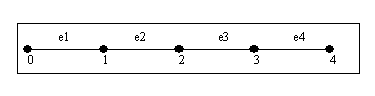
Le système algébrique à résoudre s'obtient en trois étapes :
On calcule les matrices et seconds membres élémentaires pour chaque
élément :
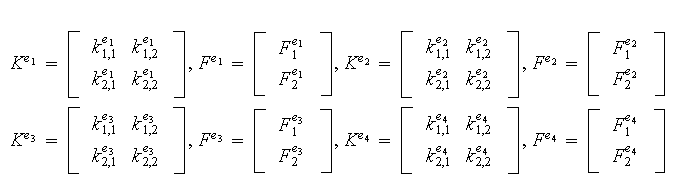
On forme la matrice

 et le second membre globales (assemblage), on obtient :
et le second membre globales (assemblage), on obtient :
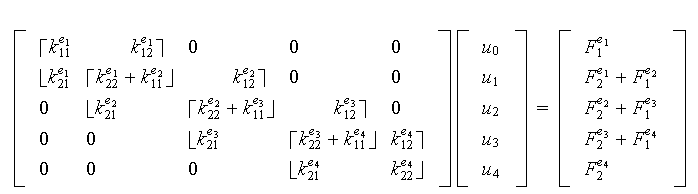
On prend en compte les conditions de Dirichlet :
On rajoute deux équations, c'est-à-dire

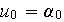 et
et

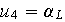 .
On obtient le système
.
On obtient le système
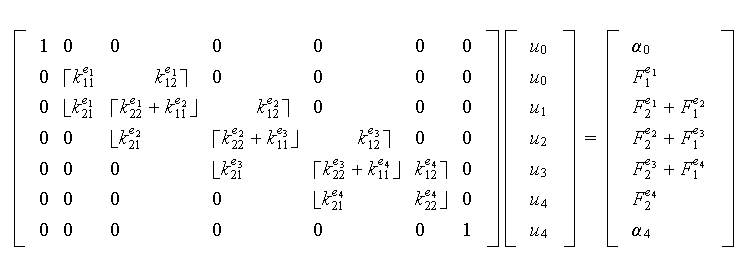
Le calcul des matrices et seconds membres élémentaires fait
intervenir des calculs d'intégrales. En général, on fait
appelle aux méthodes numériques pour les approcher. On utilisera des
formules de quadrature de type :
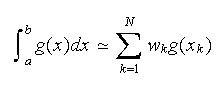
où les

![]() sont les abscisses de points choisis dans l'intervalle
sont les abscisses de points choisis dans l'intervalle

![$\left[ a,b\right] $](fem__75.png) et les
et les

![]() sont les poids correspondants. Exemple de formules de quadrature :
sont les poids correspondants. Exemple de formules de quadrature :

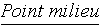 :
:

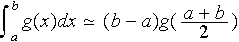 qui est exacte pour des polynômes de degré
qui est exacte pour des polynômes de degré

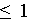 ;
;

![]() :
:

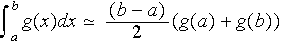 qui est exacte pour des polynômes de degré
qui est exacte pour des polynômes de degré

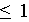 ;
;

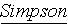 :
:

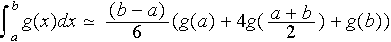 qui
est exacte pour des polynômes de degré
qui
est exacte pour des polynômes de degré

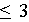 ;
;

 à 2 points :
à 2 points :

![]() où
où

 et
et

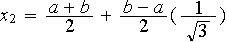 qui est exacte pour des polynômes de degré
qui est exacte pour des polynômes de degré

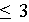 ;
;
...
| coord | : | Tableau des coordonnées des points |
| elements | : | Tableau des degrés de liberté associées a chaque élément |
| bordD | : | Tableau des degrés de liberté sur le bord de Dirichlet |
coord.dat |
elements.dat |
bordD.dat |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
| ntdl | Nombre total des degrés de liberté | |
| Numeros | Tableau des numéros des degrés de liberté inconnues |
| A | Matrice globale | |
| B | Second membre globale | |
| Ke | Matrice élémentaire | |
| Fe | Second membre élémentaire | |
| uh | Vecteur solution |
En général, la résolution par éléments finis des problèmes ci-après nécessite les programmes suivants :
| principal | Programme d'appel principal | |
| KeFe | Sous-programme de calcul de la matrice et second membre élémentaires |
La structure du programme principal est la suivante :
Chargement du maillage et informations qui lui sont relatives
Lecture des fichiers de données : coord.dat, elements.dat, bordD.dat et bordN.dat
Calcul des caractéristiques : ntdl et Numeros
Initialisations des tableaux : A, B et uh
Calcul des matrices et des seconds membres élémentaires et leurs assemblages
Prise en compte des conditions aux limites : de Neumann et (ou) de Dirichlet
Résolution du système
Présentation de la solution
%==========================================================================
% -(sigma*u')'+beta*u'+lamda*u = f, dans 0 < x < L
% u(0) = u0 et u(L) = uL
%==========================================================================
% Approximation P1
% ================
% Les fichiers de donnees :
% <coord.dat>, <elements.dat> et <bordD.dat>
% Le sous-programme :
% <KeFe.m>
% Les fonctions :
% <sigma.m>, <beta.m>, <lamda.m> et <f.m>
%-------------------------------------------------------------------------
% Descriptions des tableaux relatives au maillage
%-------------------------------------------------------------------------
%\qquad coord : coordonnees de points
% x1
% ...
% elements : degres de liberte associes a chaque element
% dl#1 dl#2 ...
% ... ... ...
%\qquad bordD : bord de Dirichlet
% noeud# dl#1 ...
% ... ... ...
%--------------------------------------------------------------------------
% A\qquad \qquad : matrice globale
% B : Second membre globale
%\qquad Ke : matrice elementaire
% Fe : Second membre elementaire
% uh : vecteur solution
% Numeros : numeros des dls inconnues
%==========================================================================\qquad
%------------------------------------------------%
% Programmeurs: B. Aoubiza & R. Laydi (an 2001) %
% Copyright (c) ENSMM %
% Universite de Franche-Comte %
%------------------------------------------------%
clc; % effacer l'ecran
clear all; % effacer toutes les variables de la section de travail.
%-------------------------------------------------------------------
% 1. Maillage et les informations qui lui sont relatives
%-------------------------------------------------------------------
% Lecture
load coord.dat ;
load elements.dat ;
load bordD.dat ;
% Calcul
ntdl = max(max(elements)); % Nombre total des degres de liberte
Numeros = setdiff(1:ntdl,bordD(:,2));% Degres de liberte inconnus
%-----------------------------
% initialisation des matrices
%-----------------------------
A = sparse(ntdl,ntdl); % matrice du systeme
B = sparse(ntdl,1); % vecteur second membre
uh = sparse(ntdl,1); % vecteur solution
%-----------------------------------------------------------------
% 2. Calcul des matrices et des seconds membres elementaires
% et leurs assemblage
%-----------------------------------------------------------------
for el=1:size(elements,1), % boucle sur les elements
noe = elements(el,:) ; % numeros des noeuds sommets
x1 = coord(noe(1)) ; % abscisse sommet 1
x2 = coord(noe(2)) ; % abscisse sommet 2
[Ke,Fe] = KeFe(x1,x2) ; % calcul de Ke et Fe
A(noe,noe)= A(noe,noe)+ Ke ; % Assemblage de A
B(noe) = B(noe) + Fe ; % Assemblage de B
end
%-------------------------------------------------------------------
% 3. Prise en compte des conditions aux limites de Dirichlet
%-------------------------------------------------------------------
dl = bordD(1,2); % Numero du degre de liberte a gauche
uh(dl) = 0 ; % Condition au bord de gauche
dl = bordD(2,2); % Numero du degre de liberte a droite
uh(dl) = 100 ; % Condition au bord de droite
% Mise a jour du second membre
B = B-A*uh;
%-------------------------------------------------------------------
% 4. Resolution du systeme
%-------------------------------------------------------------------
uh(Numeros) = A(Numeros,Numeros)\B(Numeros);
%-------------------------------------------------------------------
% 5. Presentation la solution
%-------------------------------------------------------------------
plot(coord,uh,'*');
legend('Solution approch\U{e9}e');
%---------------------------Fin-------------------------------------
function [Ke,Fe] = KeFe(x1,x2)
%-------------------------------------------------------------------
Fe = zeros(2,1); Ke = zeros(2,2);
% Abscisses et poids de Gauss-Legendre (2 points)
x(1) = (x1+x2)/2 + ((x2-x1)/2)*(-1/sqrt(3));
x(2) = (x1+x2)/2 + ((x2-x1)/2)*( 1/sqrt(3));
pg = [(x2-x1)/2 , (x2-x1)/2]; % Poid des points
% Fonctions de base et leurs derivees
N1 = (x2-x)/(x2-x1); dN1 = -1/(x2-x1)*ones(1,2);
N2 = (x-x1)/(x2-x1); dN2 = 1/(x2-x1)*ones(1,2);
% Matrice elementaire
Ke(1,1)= dot(pg , sigma(x).*dN1.*dN1+beta(x).*dN1.*N1+lambda(x).*N1.*N1);
Ke(1,2)= dot(pg , sigma(x).*dN2.*dN1+beta(x).*dN2.*N1+lambda(x).*N2.*N1);
Ke(2,1)= dot(pg , sigma(x).*dN1.*dN2+beta(x).*dN1.*N2+lambda(x).*N1.*N2);
Ke(2,2)= dot(pg , sigma(x).*dN2.*dN2+beta(x).*dN2.*N2+lambda(x).*N2.*N2);
% Second membre elementaire
Fe(1)= dot(pg , f(x).*N1); % dot : produit scalaire
Fe(2)= dot(pg , f(x).*N2);
On s'intéresse à la résolution par la méthode des
éléments finis du problème à données
régulières suivant :
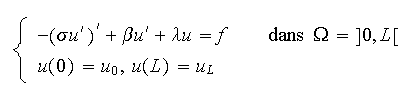
dont la formulation variationnelle est donnée par :
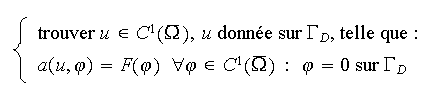
où
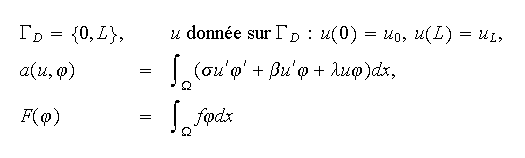

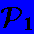
On munira

 d'une triangulation
d'une triangulation

![]() composée de
composée de

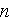 segments.
segments.


Les caractéristiques de cet élément fini sont :
Elément générique du maillage

![]() ,
,

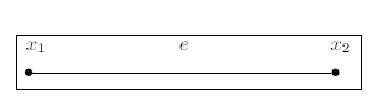
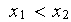 ,
,
Espace d'interpolation :

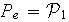 ;
;
Ensemble des degrés de liberté :

![]() où
où

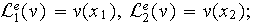
Fonctions d'interpolation :

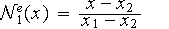 et
et 
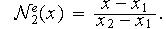
L'espace d'approximation s'écrit sous la forme
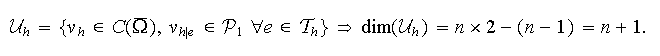
On cherche à résoudre, par l'élément fini

![]() défini
ci-dessus, le problème () avec des conditions aux limites de Dirichlet
dont la forme bilinéaire et la forme linéaire sont données par
().
défini
ci-dessus, le problème () avec des conditions aux limites de Dirichlet
dont la forme bilinéaire et la forme linéaire sont données par
().
Le problème variationnel approché est de la forme :

où

![]() désigne un sous-espace de
désigne un sous-espace de

![]() ,
de dimension finie, construit à l'aide des fonctions d'interpolation, tel
que :
,
de dimension finie, construit à l'aide des fonctions d'interpolation, tel
que :
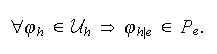
La matrice élémentaire

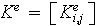

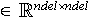 et le second membre élémentaire
et le second membre élémentaire

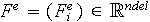 associés sont définis par
associés sont définis par
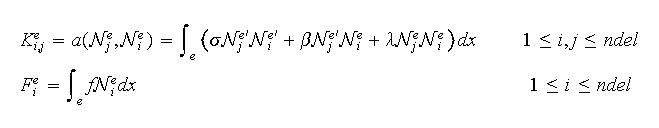
On considère la résolution du problème :
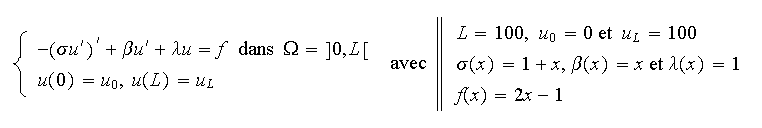

Structure des fichiers de données relatives aux maillage.
coord.dat |
elements.dat |
bordD.dat |
||||||||||||||||||||||||||||||
|
|
|
function y = sigma(x)
y = 1+x ;
function y = beta(x)
y = x ;
function y = lambda(x)
y = 1;
function y = f(x)
y = 1;
Ci-dessous le graphe de la solution approchée du problème.
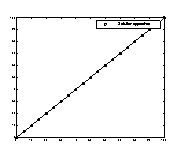

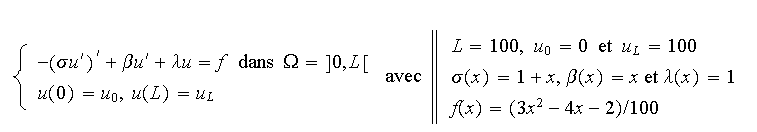
En concervant la configuration géométrique du problème ci-dessus, apporter les modifications nécess-aires aux fonctions Matlab pour résoudre ce problème.
Vérifier que

![]() est la solution du problème ci-dessus.
est la solution du problème ci-dessus.
Sur le même graphe, afficher les deux solutions (exacte et approchée). Quelles sont vos constatations sur les solutions?
On considère le problème à données régulières
suivant :
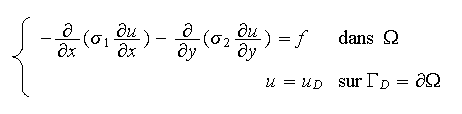
dont la formulation variationnelle est
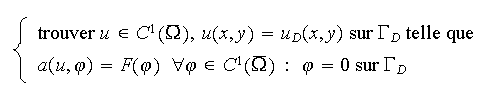
où
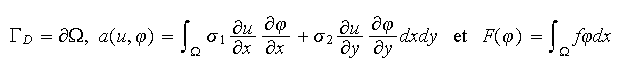

On munira

 d'une triangulation
d'une triangulation

![]() ,
composée de
,
composée de

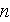 triangles. On se propose de résoudre le problème () par
l'élément fini
triangles. On se propose de résoudre le problème () par
l'élément fini

![]() .
.
Les caractéristiques de cet élément fini sont :
Elément générique du maillage : un triangle

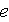 de sommets
de sommets

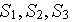

Espace d'interpolation :

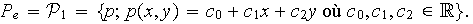
Ensemble des degrés de liberté :

![]() où
où

Fonctions d'interpolation :
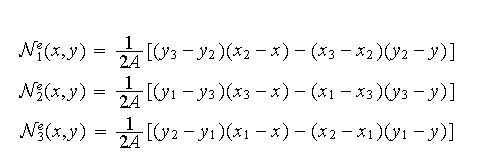
avec

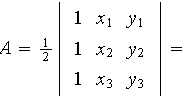 l'air
de
l'air
de

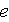
L'espace d'approximation est donc
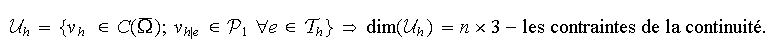
La matrice élémentaire

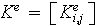

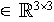 et le second membre élémentaire
et le second membre élémentaire

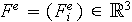 associés au problème sont définis par
associés au problème sont définis par
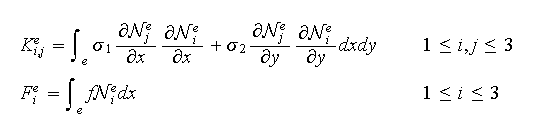
On approche le problème () par
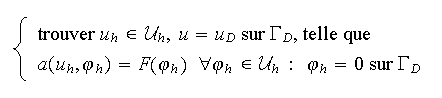
Comme dans le cas de la dimension

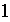 ,
nous évaluerons les intégrales à l'aide d'une formule
d'intégration approchée, de la forme :
,
nous évaluerons les intégrales à l'aide d'une formule
d'intégration approchée, de la forme :
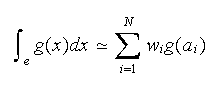
où les

![]() sont des points de l'élément
sont des points de l'élément

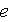 et les
et les

![]() sont les poids correspondants.
sont les poids correspondants.
Généralisation de la formule du point mileu
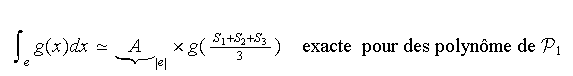
Généralisation de la formule du trapèze

Formule de Gauss-Legendre (les milieux des arêtes)
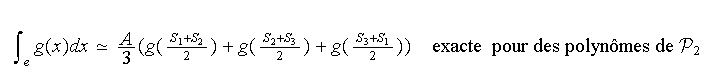
coord.dat |
elements.dat |
bordD.dat |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
On s'intéresse à la résolution du problème suivant :
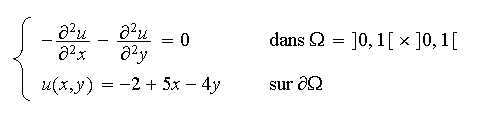
Ainsi,

![]() ,
,

![]() ,
,

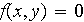 et
et

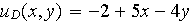 .
.
coord.dat |
elements.dat |
bordD.dat |
||||||||||||||||||||||||||||||||||||||
|
|
|
function sigma1 = sigma1(x,y)
sigma1 = 1 ;
function sigma2 = sigma2(x,y)
sigma2 = 1 ;
function f = f(x,y)
f = 0;
function ud = u_D(x,y)
ud = -2+5*x-4*y ;
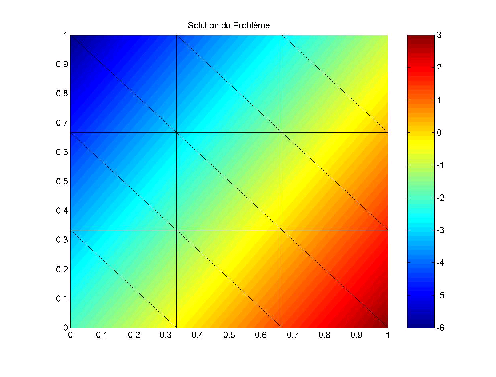
Ci-dessous, on présente les isovaleurs de la solution approchée
(
![]() ).
).
Vérifier que

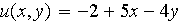 est la solution analytique du problème ;
est la solution analytique du problème ;
Comparer les deux solutions en apportant les modifications nécessaires au programme ;
Que constatez-vous?
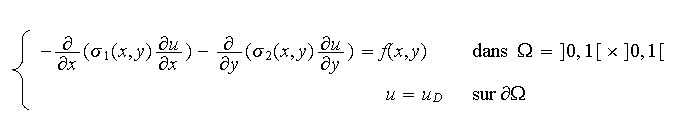
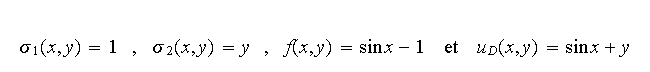
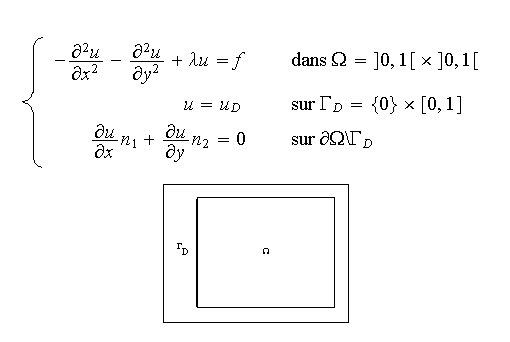
Donner la formulation variationnelle de ce problème ;
Apporter les modifications nécessaires aux fonctions
Matlab pour résoudre ce problème avec les
données suivantes :
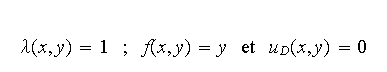
%======================================================================
% - div(sigma_i(x,y).grad(u))= f dans Omega
% u(x,y) = uD sur bordD
%======================================================================
% Approximation P1
% ================
%------------------------------------------------%
% Programmeurs: B. Aoubiza & R. Laydi (an 2001) %
% Copyright (c) ENSMM %
% Universite de Franche-Comte %
%------------------------------------------------%
clc; % effacer l'ecran
clear all; % effacer toutes les variables de la section de travail.
%-------------------------------------------------------------------
% 1. Maillage et les informations qui lui sont relatives
%-------------------------------------------------------------------
% Lecture
load coord.dat ;
load elements.dat;
load bordD.dat ;
% Calcul
ntdl = max(max(elements(:,:))) ; % Nombre total des degres de liberte
Numeros=setdiff(1:ntdl,bordD(:,2)); % Degres de liberte inconnus
%-----------------------------
% initialisation des matrices
%-----------------------------
A = sparse(ntdl,ntdl); % matrice du systeme
B = sparse(ntdl,1); % vecteur second membre
uh = sparse(ntdl,1); % vecteur solution
%-----------------------------------------------------------------
% 2. Calcul des matrices et des seconds membres elementaires
% et leurs assemblage
%-----------------------------------------------------------------
for el=1:size(elements,1), % boucle sur les elements
npt = elements(el,:) ; % numeros des points sommets
ex = coord(npt,1) ; % abscisses
ey = coord(npt,2) ; % ordonnees
noe = elements(el,:) ; % numeros des dl de l'element
[Ke,Fe] = KeFe(ex,ey) ; % calcul de Ke et Fe
A(noe,noe) = A(noe,noe) + Ke ; % assemblage de la matrice
B(noe) = B(noe) + Fe ; % assemblage du second membre
end
%-------------------------------------------------------------------
% 3 Prise en compte des conditions aux limites de Dirichlet
%-------------------------------------------------------------------
for i=1:size(bordD,1), % Nombre de degre de liberte sur GammaD
npt = bordD(i,1) ; % Numeros du point
dl = bordD(i,2) ; % Numeros du degre de liberte
xy = coord(npt,:) ; % x y du point
uh(dl)= uD(xy(1),xy(2));
end
% Mise a jour du second membre
B = B-A*uh ;
%-------------------------------------------------------------------
% 4. Resolution du systeme
%-------------------------------------------------------------------
uh(Numeros) = A(Numeros,Numeros)\B(Numeros);
uh=full(uh);
%-------------------------------------------------------------------
% 5. Presentation de la solution
%-------------------------------------------------------------------
% Une presentation graphique de la solution approchee
trisurf(elements,coord(:,1),coord(:,2),uh','facecolor','interp');
view(0,90);
title('Solution du Probleme');
colorbar;
%---------------------------Fin-------------------------------------
function [Ke,Fe] = KeFe(ex,ey)
%------------------------------------------------------------------------
% Calcul de la matrice et du second membre elementaire
%------------------------------------------------------------------------
% Entree : coordonnees des sommets de l'element
% ex = [x1 x2 x3]
% ey = [y1 y2 y3]
% Sortie : Ke : Matrice elementaire (3 x 3)
% Fe : Second membre elementaire (3 x 1)
%------------------------------------------------------------------------
% On utilise la methode de Gauss-Legendre avec 3 points.
A=0.5*det([ones(3,1) ex ey]); % Aire du triangle
% Points d'integration : milieux des arretes
x =0.5*[ex(2)+ex(1) ex(3)+ex(2) ex(1)+ex(3)];
y =0.5*[ey(2)+ey(1) ey(3)+ey(2) ey(1)+ey(3)];
pg=[A/3 , A/3 , A/3]; % Poids des points
%
% Fonctions de base aux 3 points d'integration
%
N1 = ((ey(3)-ey(2)).*(ex(2)-x)-(ex(3)-ex(2)).*(ey(2)-y))/(2*A);
N2 = ((ey(1)-ey(3)).*(ex(3)-x)-(ex(1)-ex(3)).*(ey(3)-y))/(2*A);
N3 = ((ey(2)-ey(1)).*(ex(1)-x)-(ex(2)-ex(1)).*(ey(1)-y))/(2*A);
%
% Derivees des fonctions de base aux 3 points d'integration
%
dxN1=-(ey(3)-ey(2))/(2*A)*ones(1,3); dyN1=(ex(3)-ex(2))/(2*A)*ones(1,3);
dxN2=-(ey(1)-ey(3))/(2*A)*ones(1,3); dyN2=(ex(1)-ex(3))/(2*A)*ones(1,3);
dxN3=-(ey(2)-ey(1))/(2*A)*ones(1,3); dyN3=(ex(2)-ex(1))/(2*A)*ones(1,3);
%===========================
% Matrice elemantaire %
%===========================
Ke(1,1) = dot(pg , sigma1(x,y).*dxN1.*dxN1+sigma2(x,y).*dyN1.*dyN1);
Ke(1,2) = dot(pg , sigma1(x,y).*dxN2.*dxN1+sigma2(x,y).*dyN2.*dyN1);
Ke(1,3) = dot(pg , sigma1(x,y).*dxN3.*dxN1+sigma2(x,y).*dyN3.*dyN1);
Ke(2,1) = dot(pg , sigma1(x,y).*dxN1.*dxN2+sigma2(x,y).*dyN1.*dyN2);
Ke(2,2) = dot(pg , sigma1(x,y).*dxN2.*dxN2+sigma2(x,y).*dyN2.*dyN2);
Ke(2,3) = dot(pg , sigma1(x,y).*dxN3.*dxN2+sigma2(x,y).*dyN3.*dyN2);
Ke(3,1) = dot(pg , sigma1(x,y).*dxN1.*dxN3+sigma2(x,y).*dyN1.*dyN3);
Ke(3,2) = dot(pg , sigma1(x,y).*dxN2.*dxN3+sigma2(x,y).*dyN2.*dyN3);
Ke(3,3) = dot(pg , sigma1(x,y).*dxN3.*dxN3+sigma2(x,y).*dyN3.*dyN3);
%============================
% Second membre elementaire %
%============================
Fe(1,1) = dot(pg , f(x,y).*N1) ;
Fe(2,1) = dot(pg , f(x,y).*N2) ;
Fe(3,1) = dot(pg , f(x,y).*N3) ;This document created by Scientific WorkPlace 4.0.